はじめに

この記事では、データ分析プロセスの全体像を読み、ベースラインとなるモデルを作成することの大切さを学んだ方を対象としております。ベースラインとなるモデルを作成し、評価を行った際に数値的に良い精度になることもあれば、想定より悪い精度になることもあるかと思います。この際に、以下のような判断をすることが多いと思います。

• 良い精度が出たなら、そのままのモデルを採用しよう。
• 想定より悪い精度だから、モデルを作り直そう。

後者の場合、モデルとそのハイパーパラメーター、変数の選択などモデルの作り方を根本的に見直す方向性で判断することになるでしょう。しかし、前者であってもモデルの妥当性については一定の注意・検証を行う必要があるため、本記事では前者に注目し、なぜ現状のベースラインモデルで精度が出ているのかを一歩踏み込んで考えるための観点をお伝えします。

データの設計は適切か？

ベースラインモデルの精度が悪い時であれば、適切にデータが設計されているかどうかを再度確認しようと考えやすいでしょう。図でいうところの（2）と（4）のケースに当たります。

一方で、不適切なデータ設計であるにもかかわらず、精度が良い場合は見過ごすリスクが高いでしょう。図で言うところの（3）のケースに当たります。

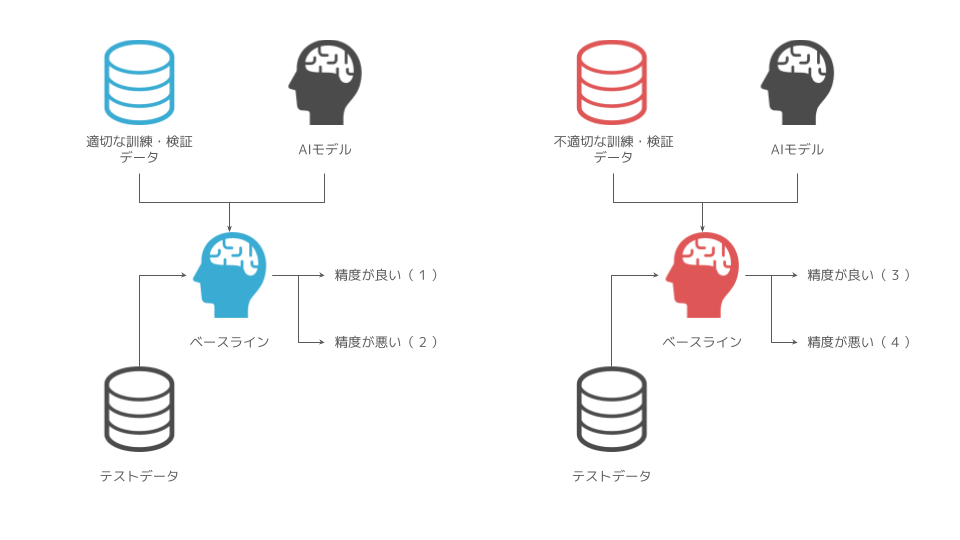
ここで、不適切なデータ設計とは具体的にどのような状況を意味するのかを考えるために、データ分割に立ち戻って考えてみます。

ホールドアウト法の記事の通り、AI モデル作成に用いるデータは一般的に以下 3 つに大別され、手元のデータを目的別に分割します。

• 訓練データ
  • モデル学習に用いるデータ
• 検証データ
  • 訓練データを使って学習したモデルの中で最も良いモデル（説明変数とハイパーパラメータの組み合わせ）を選択するために用いるデータ
• テストデータ
  • 検証データを使って選択したモデルが未知のデータに対してどのくらい精度が出せるか(実運用に耐えられるか)を測るために用いるデータ

訓練データと検証データをまとめて、ここでは学習データと呼ぶことにします。分割の仕方が不適切な場合、分割されたデータは目的を達成できなくなります。特に時系列データを分析する場合には、記事に示したリークなどの事象については、分析者が意識的に起こらないように注意できるでしょう。

過学習していないか？

過学習とは、ベースラインのモデルが学習データの特徴を過度に捉えてしまっている状況を意味します。

本来、モデル化は説明変数と目的変数の特徴を捉え、ある程度の誤差はありつつも説明変数と目的変数のデータ間の関係性を表現するために行われます。そのため、過学習しており、うまくデータを象徴できていない AI モデルに対しては、汎化性能が低いと表現されます。

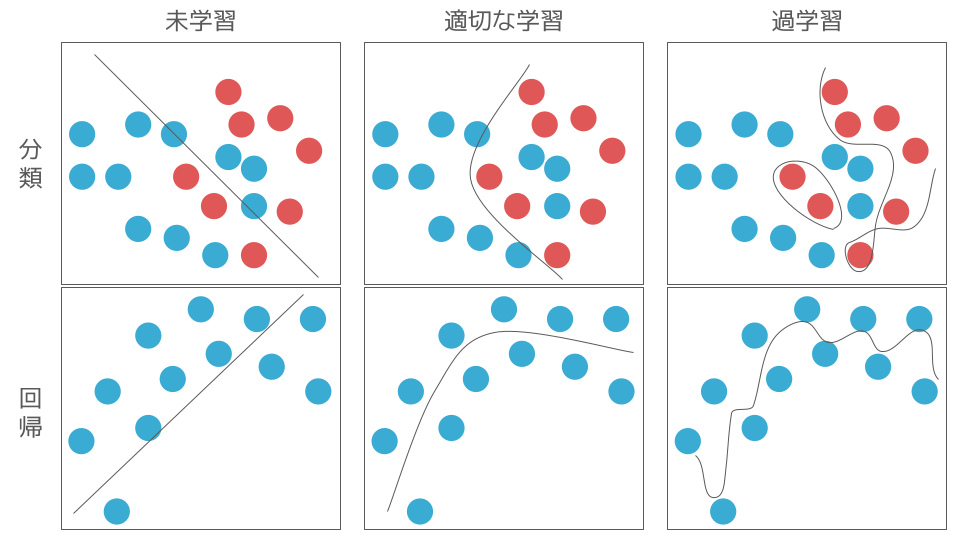
以下の図は、分類と回帰に関する学習状況の具体的なイメージを表しております。 過学習している場合、モデルは学習データの細部まで特徴を捉えすぎていることがわかります。 このため、学習データに対する誤差は非常に小さくなりますが、テストデータに対する誤差は大きくなる傾向があります。 これは、モデルが学習データのノイズにまで適合してしまい、汎化性能が低下するためです。

一方、適切な学習をしている場合、モデルは学習データ全体の大まかな傾向を捉え、特定のデータに過度に適合しないように調整されます。

この場合、学習データに対する誤差は適度に小さく保たれ、テストデータに対する誤差も比較的小さい値を取ります。そのため、適切な学習をしているモデルの方が過学習しているモデルよりも汎化性能が高いと言えるでしょう。

しかし、ベースラインのモデルが適切に学習できているかをテストデータに対する精度だけで判断してしまうと以下の状況に陥るリスクがあります。

• 学習データ、テストデータに対する当てはまりは良いが、手元にあるデータ以外の未知のデータに対する当てはまりが悪くなってしまっている状況

この場合、検証データとテストデータで分布が似ているため精度が高いベースラインモデルが作成できたと考えやすいですが、根本的な問題として考えられるのは、未知のデータとの差分が大きいことです。

ホールドアウト法を用いた場合で、データの分割パターンが 1 つに固定化された上で評価されてしまい、たまたま検証データとテストデータの傾向が似てしまっていると汎化性能が落ちる可能性があります。

そのため、データ分割のアプローチがモデル選定に影響を及ぼすことを考慮する必要があり、代表的なデータ分割のアプローチについてメリット・デメリットを把握することは非常に重要です。

• ホールドアウト法
  • メリット
    • 交差検証法と比較して、モデル選定時の計算コストが低い
  • デメリット
    • 1 つのデータ分割パターンのみでモデルを選定するため、モデルの汎化性能が低くなりやすい
• 交差検証法（クロスバリデーション）
  • メリット
    • ホールドアウト法と比較して、過学習を起こしにくい
  • デメリット
    • ホールドアウト法と比較して、複数のデータ分割パターンでモデルを選定するため、モデルの汎化性能が高くなりやすい

明らかにデータの特徴として、周期性があることがわかりきっている場合であれば、ホールドアウト法で評価することでダイレクトに特徴を捉えられる可能性はありますが、多くの場合そのようなケースは少ないことが容易に考えられます。

そのため、交差検証法（クロスバリデーション）を用いることで、複数の分割パターンの組み合わせで評価することで、ベースラインモデルに対してより適切な評価ができることが期待されます。

ホールドアウト法と交差検証法の違いを以下に図示しました。

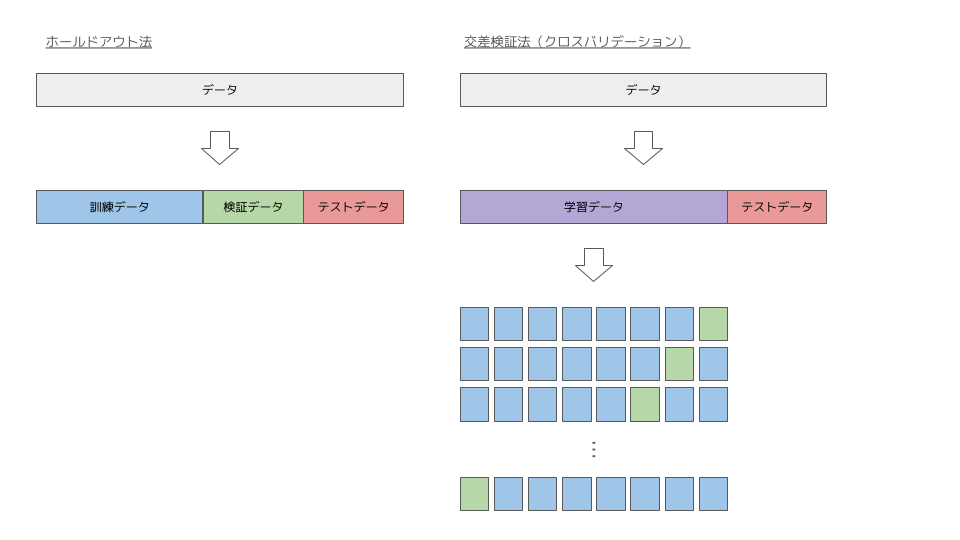
図はテーブルデータに対するホールドアウト法と交差検証法を示しております。検証データは、訓練データの説明変数とハイパーパラメータの組み合わせて学習されたモデルの中から精度の良いモデルを 1 つ選択するために用いられます。

そのため、学習モデルと検証の組み合わせパターンが 1 つのみのホールドアウト法と学習モデルと検証の組み合わせパターンが複数の交差検証法では、交差検証法の方が汎化性能の高いモデルを選定できることは直感的にもわかるかと思います。

また、テーブルデータに対する交差検証法では学習データと検証データの順序は関係ありませんが、時系列データでは「過去のデータで予測モデルを学習し、未来の目的変数を予測する」という前提を満たす形で、データを分割することが求められます。

時系列データの交差検証法には、2 種類あることが知られております。

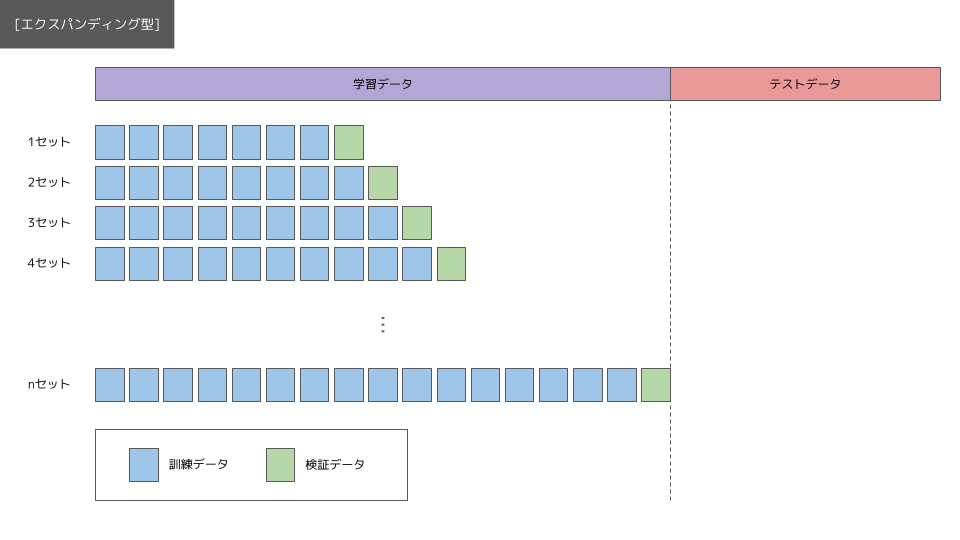
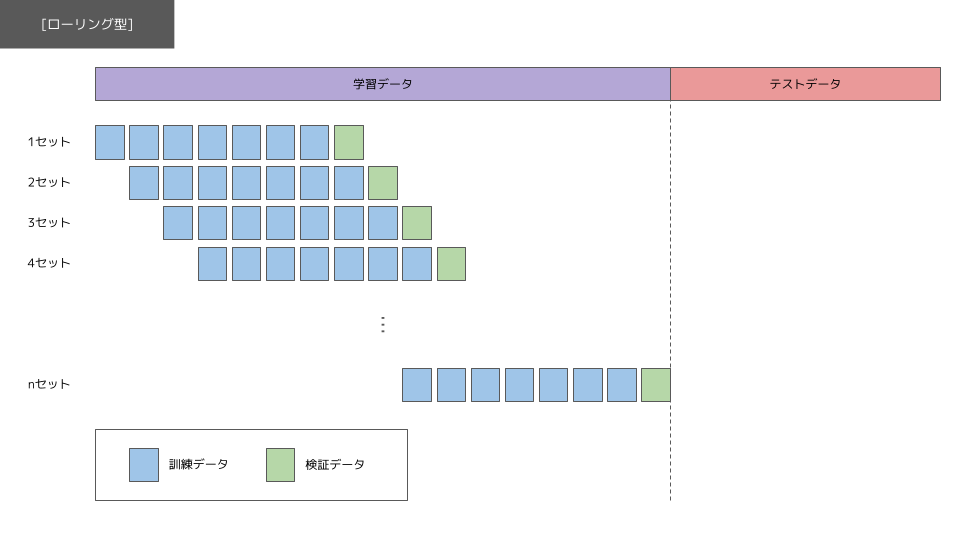
エクスパンディング型は、定められた学習データの範囲内で訓練データのデータ数を徐々に大きくしながらモデルを適合させていくアプローチになります。ローリング型は定められた学習データの範囲内で訓練データと検証データの期間をずらしながらモデルを適合させていくアプローチになります。

まとめ

• データの設計により、見かけ上評価時の精度が高くなっていないかに注意しましょう。特に時系列データの場合、時間の前後関係を注意しながらデータを設計・分割する必要があるため、データの特性に合わせた設計を心がけましょう。
• 過学習により、見かけ上評価時の精度が高くなっていないかに注意しましょう。
• 評価を行う際には、データの特徴と一般的なデータ分割アプローチのメリット・デメリットを踏まえて、ホールドアウト法や交差検証法などのアプローチを選定しましょう。
• 時系列データで交差検証法を行う際には、データの時間順序を考慮した設計を前提としており、具体的に 2 つのアプローチがあります。

参考文献

• 髙橋 (2023). Python による時系列分析 ―予測モデル構築と企業事例-. オーム社.