はじめに

モデルの評価指標として用いられる、相関係数(CORR)と決定係数(R2)について解説します。 本ページと合わせてモデル評価(MAE/RMSE)を読むとモデルの評価方法について深く理解できます。

相関係数と決定係数を解説しますが、モデル評価には基本的に決定係数を用います。 相関係数はビジネスの場面でも多く使われる指標であり、多くの方にとって理解しやすいものです。 そのため、相関係数をモデル評価に使う場面としては、ビジネス側のステークホルダーと話す際にビジネス側の納得感を上げるために使うことが多いです。

相関係数(CORR)

相関係数(CORR:Correlation Coefficient) は、2 つの変数間の直線的な関係の強さと方向を表す$-1 \leqq r \leqq 1$の範囲の数値です。 $-1 \leqq r \leqq 0$の時「変数間は負の相関」（一方の値が増加すると一方の値は減少する）ような関係性があり、 $0 \leqq r \leqq 1$の時「変数間は正の相関」（一方の値が増加すると一方の値も増加する）ような関係性を、 $r=0$の時「変数間に相関がない」（2 つの変数には直線的な関係がない）ことを示します。

相関係数の求め方は、$x = (x_{1}, x_{2}, \dots, x_{N})$ と $y = (y_{1}, y_{2}, \dots, y_{N})$ の共分散をそれぞれの変数の標準偏差で割って計算します。 下記に相関係数の定義を示します。

$$ \begin{eqnarray} r &=& \frac{s_{xy}}{s_{x}s_{y}} &=& \frac{{\frac{1}{N}}{\sum^N_{i=1}(x_i - \bar{x})(y_i - \bar{y})}}{\sqrt{\frac{1}{N}\sum^N_{i=1}(x_i - \bar{x})^2}{\sqrt{\frac{1}{N}\sum^N_{i=1}(y_i - \bar{y})^2}}} \end{eqnarray} $$

$s_{xy}$は$x$と$y$の共分散
$s_{x}$は$x$の標準偏差
$s_{y}$は$y$の標準偏差
$N$は$(x,y)$の総数
$\bar{x}, \bar{y}$はそれぞれ$x,y$の平均値

相関係数を用いたモデル評価

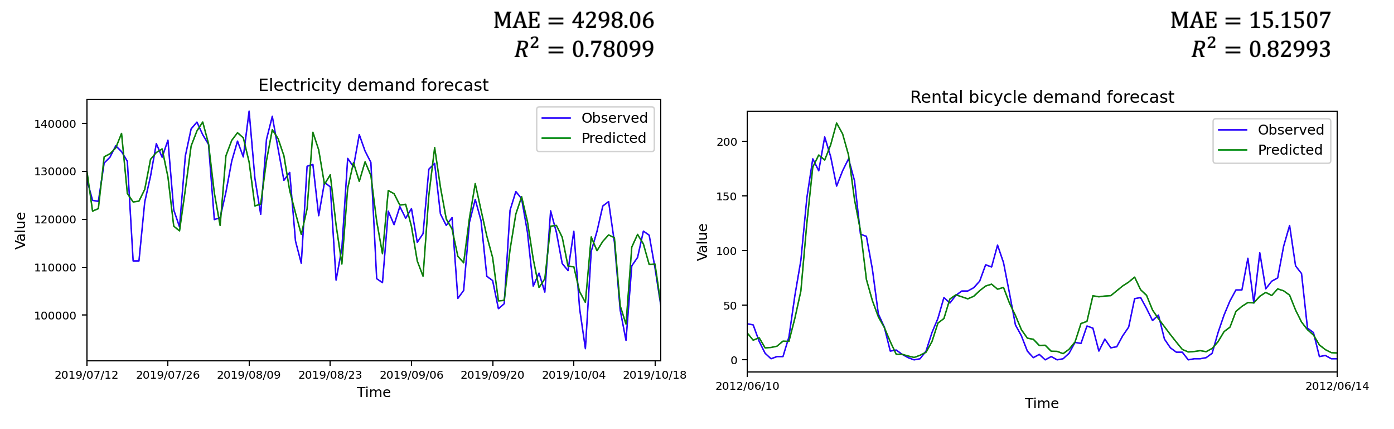
相関係数は、EDA の際に二変数間の関係性を確認するために活用されることが多いですが、モデル評価にも活用できます。 モデル評価の際には、予測値 $\hat{y}$ と実測値 $y$ を対象に、評価データの期間で相関係数を計算し、予測値が実測値にどの程度適合しているかを評価します。

データ分析プロジェクトでは、指標としてのわかりやすさからビジネス側のステークホルダーに対してモデルの当てはまりの良さを説明する際に利用することがあります。

決定係数($R^2$)

決定係数(Coefficient of determination、$R^2$) は回帰モデルの推定結果の当てはまりの良さを評価する評価指標です。 通常 $0 \leqq R^2 \leqq 1$ の範囲を取りますが、非線形モデルを使用した場合や、学習データと評価データの傾向が大きく違う場合に負の値を取ることがあります。

決定係数は以下で定義します。

予測値 $\hat{y} = (\hat{y_{1}}, \hat{y_{2}}, \dots, \hat{y_{N}})$、 実測値 $y = (y_{1}, y_{2}, \dots, y_{N})$ として下式に定義を示します。

$$ R^2 = 1 - {\frac{\sum^N_{i=1}(y_i - \hat{y_i})^2}{\sum^N_{i=1}(y_i - \bar{y})^2}} $$

$N$は$(\hat{y},y)$の総数
$\bar{y}$は$y$の平均値

決定係数を用いたモデル評価

決定係数を用いてモデルを評価する際には、予測値が実測値にどれくらい当てはまるかの割合（$0 \leqq R^2 \leqq 1=100％$、負の値の場合もあり）と解釈するとイメージしやすいです。 $1$に近づくほど、当てはまりが良いことを意味しており、モデル改善としては$0.7<0.9$の範囲であれば、十分当てはまっていると考えられます。

回帰モデルの予測値が実測値に対してどの程度当てはまっているかをわかりやすく解釈できるので、モデルの精度改善において重宝します。 一般に $0 \leqq R^2 \leqq 1$ の間の値を取ることから、MAE や RMSE のような指標とは異なり、スケールの影響を受けません。 そのため、どのようなデータや問題設定に対しても、分析者として常に同じように解釈できる指標となっています。

データ分析プロジェクトでは、モデル評価の良し悪しを、決定係数の値だけで判断するのではなく、MAE や RMSE と合わせて評価することが望ましいです。 というのも、データ分析プロジェクトはどんな問題設定であれ、ビジネス価値を生み出すために行うものです。 そのため、MAE や RMSE のようなビジネス価値を数値化し、その効果を推定できるような指標を用いることがプロジェクトの進行において重要となります。 決定係数はビジネス価値を評価する指標ではなく、データの当てはまり具合を評価する指標ですので、 MAE や RMSE といった指標と合わせて使うことで、モデル評価の納得感を補強するような指標と考えるのが良いと思います。

モデル評価における相関係数と決定係数の注意点

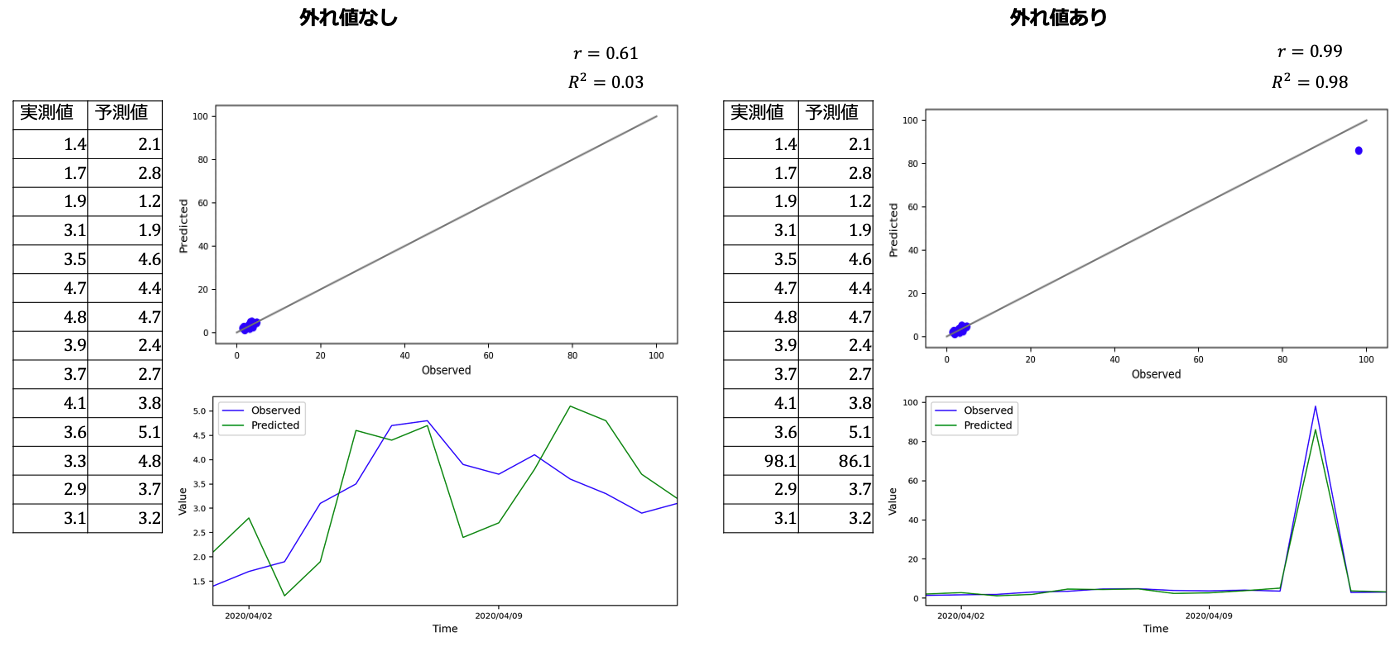
相関係数は、二変数間の直線的関係の強さと方向を表す指標でした。 そのため、外れ値の影響を大きく受ける場合があり注意が必要です。

外れ値がある場合、目的変数がいくつかのクラスターに分かれているような分布になることがあります。 そこで、予測値と実測値を散布図と時系列でプロットしたものを用いて、外れ値の影響を確認します。 下図から確認できるように、相関係数を扱う際には、外れ値の影響で相関係数が高くなることが確認できます。 また、決定係数においても数値の向上が確認できることから、同様に外れ値の影響を考慮する必要があります。

外れ値の考慮はここだけに限った話ではなく分析全体に関わる話ですが、 モデル評価の場合においても、予測値と実測値の散布図を確認した方が良いかと思います。

参考文献

• 高柳 (2023). 評価指標入門〜データサイエンスとビジネスをつなぐ架け橋. 技術評論社.