• Top
  • 適切な特徴量を考えてみた（1）

contents-thumb
  • 編集日

    2024年4月

  • カテゴリ

    分析ヒント

はじめに

AI モデルを開発した際に、どれくらいの精度が出せているのかは AI を検証する上で大切な観点です。
こちらの 記事 では、実際に精度改善を行うにあたって、どのような流れで進めていけば良いかについて記載されております。
精度改善方法にはいくつかの方向性がありますが、今回はタイトルの通り 「適切な特徴量を検討する」 方向性で精度改善を試みた記事になります。

特徴量を検討するとは

特徴量を検討するとは、手元にあるデータを加工したり、外側からデータを持ってきて、既存データ列に追加することで、学習方法は変えずに学習する説明変数のパターンを複数検討し、予測精度が向上しているのかを検証することを意味します。このような特徴量の検討は、特徴量エンジニアリングと呼ばれることが多いようです。実際に、Node-AI を使って特徴量を検討してみたいと思います。

データの概要

本記事では、 「シェアサイクル利用の総台数予測」 のデータを対象とします。 まず、データの概要を知るために、データの各カラムが何を表しており、どのような値を取るのかを把握してみようと思います。 どのカラムを目的変数とし、説明変数とすべきかを決めるためにもデータの概要を知ることは重要な営みです。 データのカラムとしては以下のようなものがあります。

  • dteday : 日付
  • season : 季節 (1:春, 2:夏, 3:秋, 4:冬)
  • yr : 年 (0:2011、1:2012)
  • mnth : 月(1〜12)
  • hr : 時間(0〜23)
  • holiday : 休日の判定
  • weekday : 曜日
  • workingday : 平日は 1、土日祝日は 0
  • weathersit :
    • 1 : 晴れ～少しの雲
    • 2 : くもり
    • 3 : 小雨
    • 4 : 大雨
  • temp : 気温
  • atemp: 体感温度
  • hum：湿度
  • windspeed：風速
  • casual：このシェアサイクルの非会員の自転車利用数
  • registered：このシェアサイクルの会員の自転車利用数
  • cnt: 自転車利用の総台数 (casual と registered の合計)

データのカラムを確認したところ、目的変数として良さそうなカラムは casual, registered, cnt のいずれかであることがわかりました。 一旦、今回は非会員から会員になる人を増やせると企業としては収益が上がることが想定されるため、casual を目的変数にしたいと思います。

分析

1回目

一旦、自転車利用数に関係しそうな説明変数を以下の内容で設定しました。

  • weathersit :
    • 1 : 晴れ～少しの雲
    • 2 : くもり
    • 3 : 小雨
    • 4 : 大雨
  • temp : 気温
  • atemp: 体感温度
  • hum：湿度
  • windspeed：風速

上記設定で実行したところ、決定係数は 0.324 であり、RMSE は 47.006 という結果になりました。

評価（1回目）

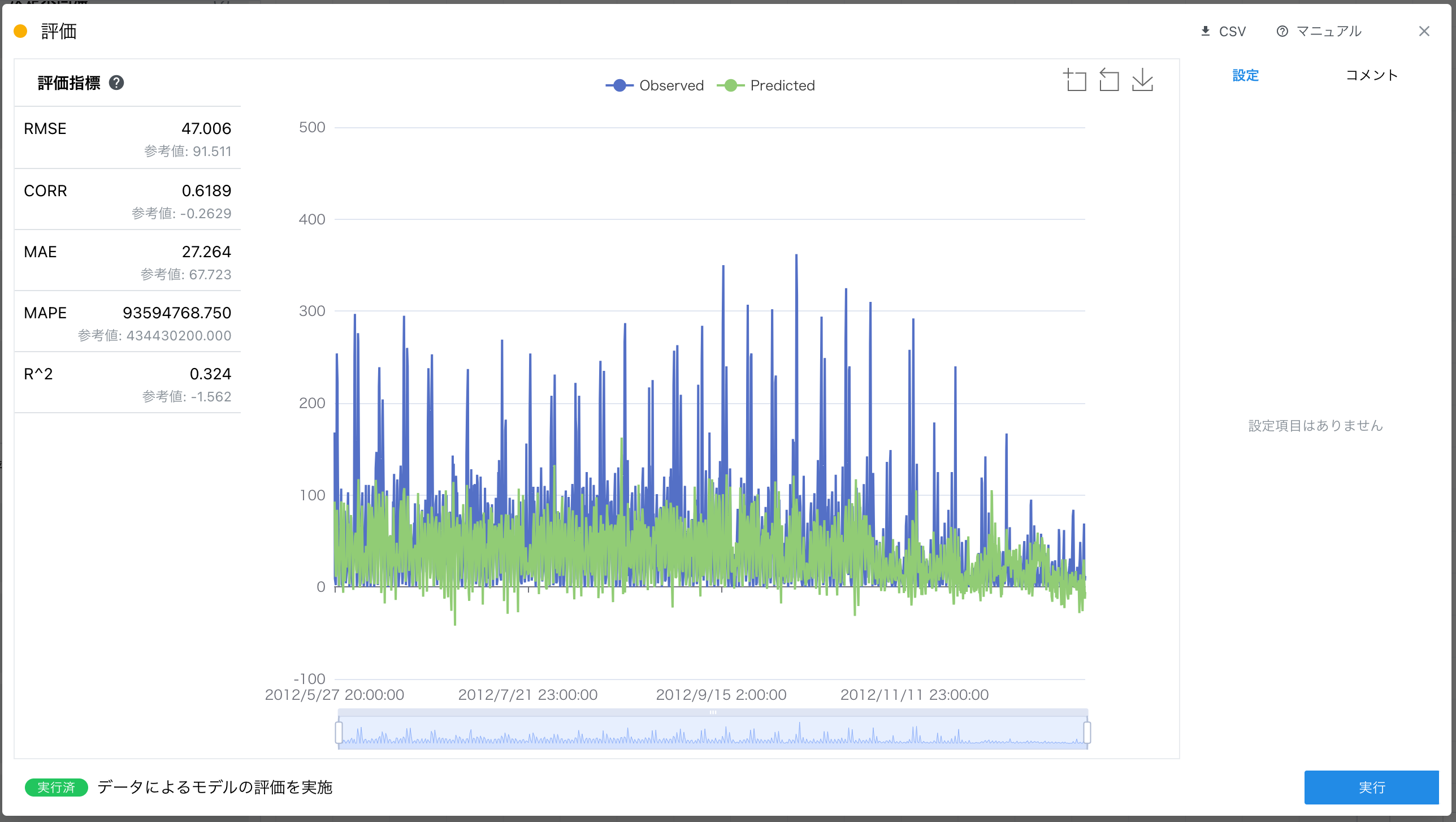
決定係数は絶対的な基準はありませんが、0.5 を超えると当てはまりが良いとされることが多いため、もう少し決定係数の値を向上させたいと考え、説明変数を見直すことにします。

時系列分析では、季節性や周期的なトレンドに注目したモデルが多いため、そのような説明力が高い変数がないかを検討したいと考え、以下を追加しました。

  • season : 季節 (1:春, 2:夏, 3:秋, 4:冬)
  • holiday : 休日の判定
  • weekday : 曜日
  • workingday : 平日は 1、土日祝日は 0

似たような意味を表す変数は、多重共線性と呼ばれる精度悪化につながることが一般的に知られているため、説明変数から以下を外すことにしました。

  • atemp: 体感温度（temp に近いデータ）
  • holiday : 休日の判定（workingday に近いデータ）

文字面だけでなく念の為、相関行列を可視化し、確認しておきます。

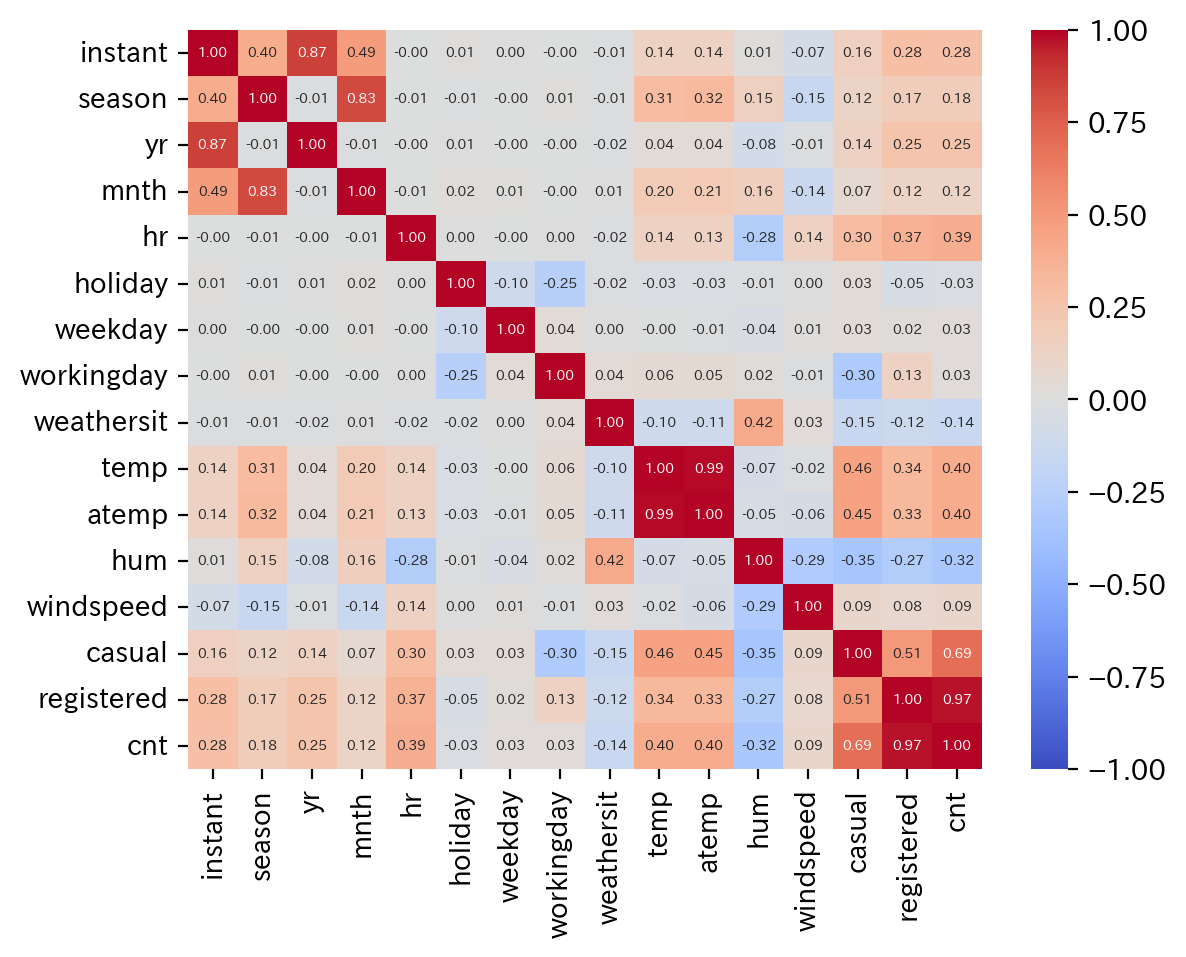相関行列ヒートマップ tempとatempは相関係数0.99になっており、相関が高いことがわかります。

2回目

説明変数を以下として実行したところ、決定係数は 0.603 であり、RMSE は 36.039 という結果になりました。

評価（2回目）

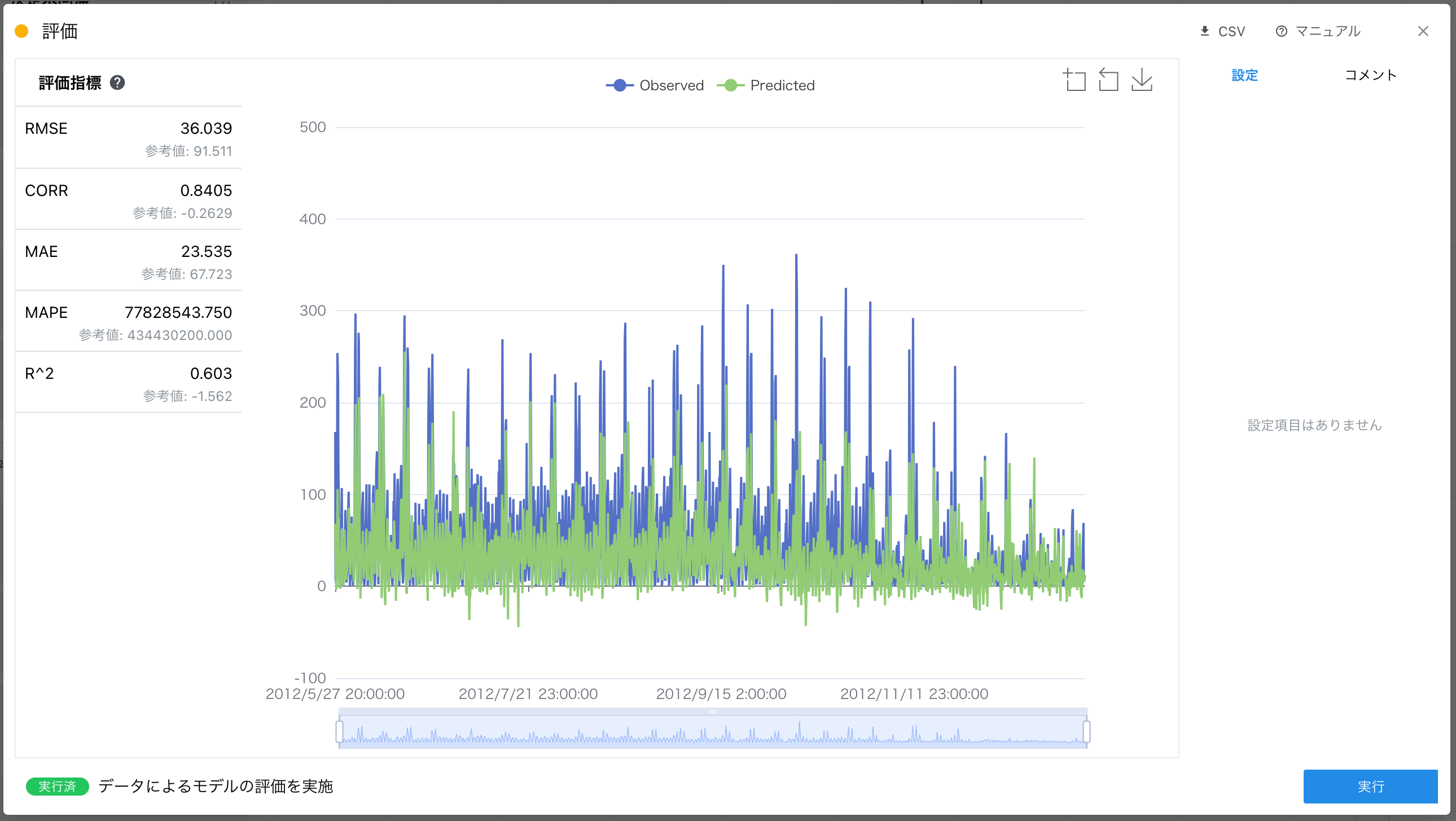
精度比較

1 回目と 2 回目を比較すると、決定係数の値は約 2 倍近い値に改善されました。

単純に説明変数の個数を増やしたことも考えられますが、増やしたデータが説明力を上げてくれたようにも思います。

こちらのチュートリアルでは、非会員と会員両方の自転車の総利用台数(cnt)に対して、バイオリンプロットを作成し、平日と休日で総利用台数に違いがあることがわかりました。

同様に、今回の分析で目的変数としていた非会員の自転車の総利用台数（casual）に関するバイオリンプロットでも同じような違いが見られるかを検証します。

バイオリンプロット（casual）

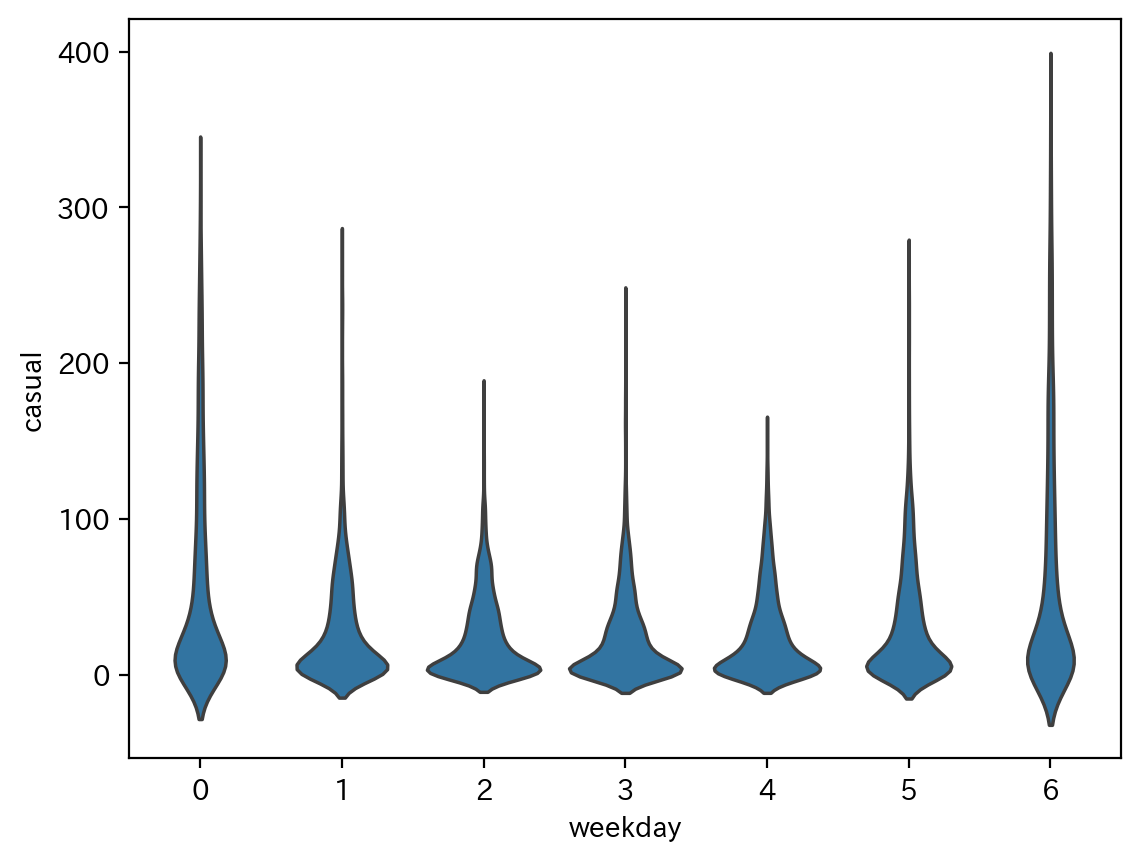
パッと見ると、異なる傾向のように考えられますが、これは外れ値による問題と考えることができそうです。非会員の自転車の総利用台数（casual）の要約統計量を確認してみると、75％点が 48 で最大値が 367 になっております。標準偏差 49.305 になっております。

要約統計量（casual）

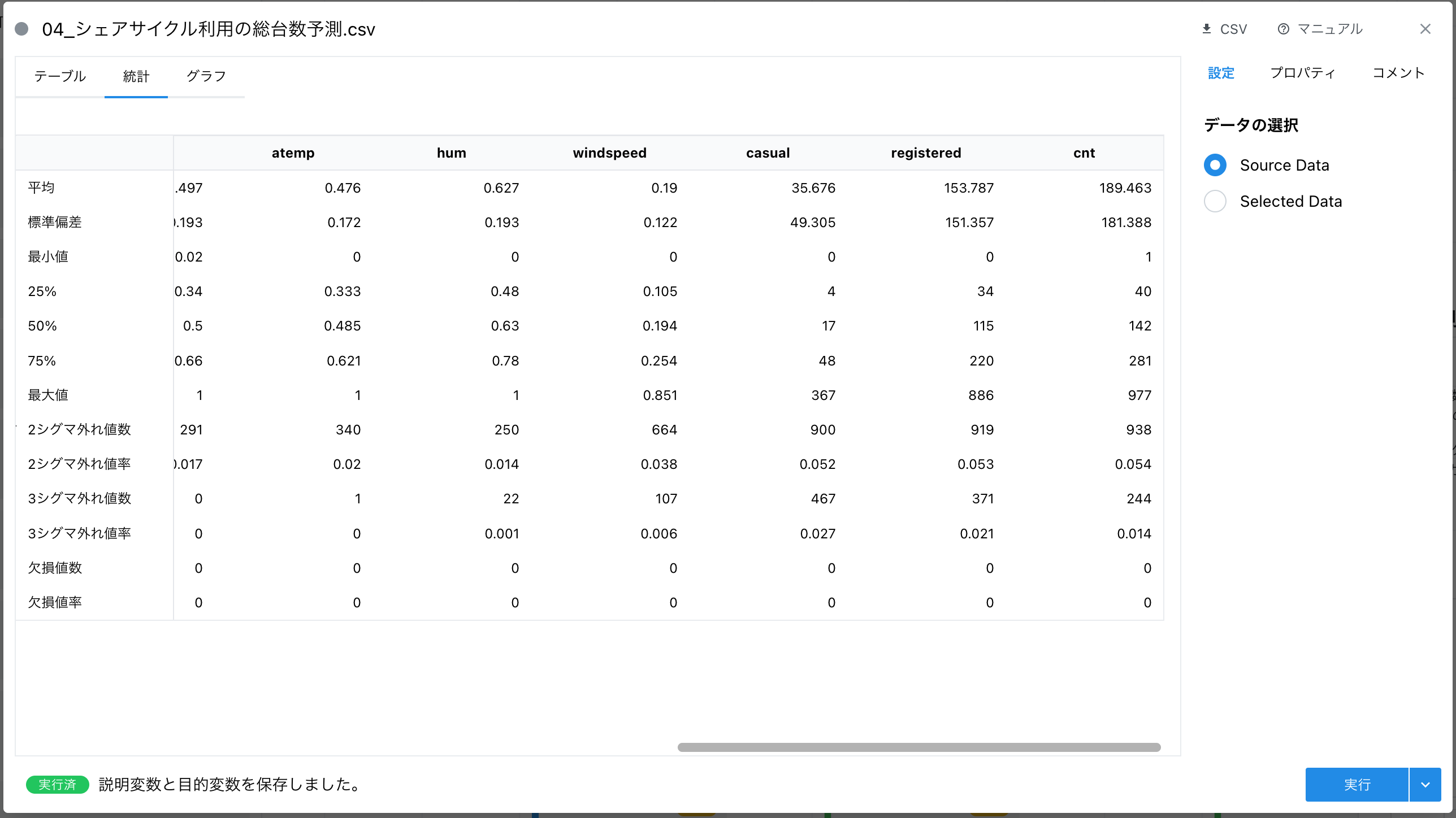
さらに、非会員の自転車の総利用台数（casual）に関するヒストグラムを見てみましょう。

ヒストグラム（casual）

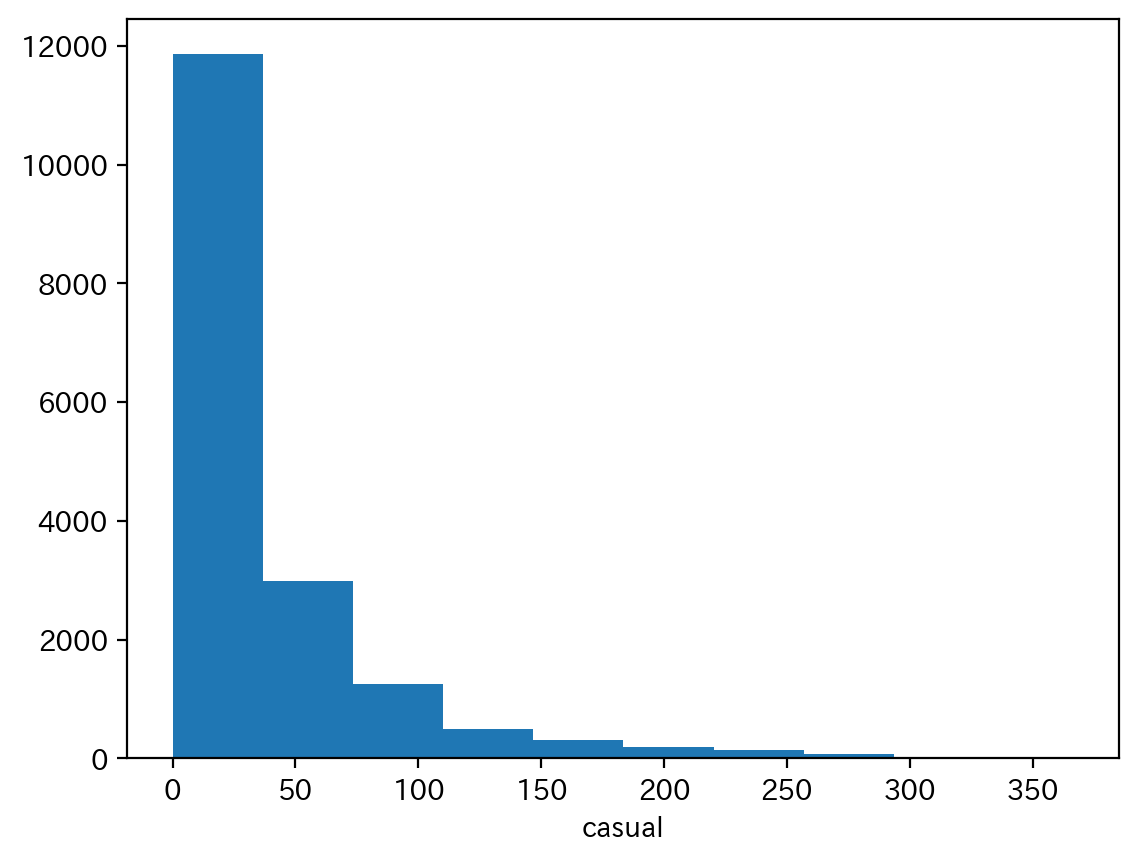
これをみると、非会員の自転車の総利用台数（casual）が 180 以上の値を取ることはほとんど無さそうですので、そのような外れ値を除くことで全体の傾向と大まかに一致することが想像できます。

そのため、下記の変数を追加することで精度向上に貢献できたと考えられます。

  • season : 季節 (1:春, 2:夏, 3:秋, 4:冬)
  • holiday : 休日の判定
  • weekday : 曜日
  • workingday : 平日は 1、土日祝日は 0

考察・感想

精度を上げるためのアイデアとして、天気に関する情報を追加することが考えられます。天気の良し悪しによって、自転車の利用数に影響が出てきそうだという仮説が立てられそうだと考えたためです。

また、地域・エリア、利用時の走行距離、自転車ステーションの設置場所などの情報が追加できるとよりビジネス課題の解決に向けて意味のある分析になりそうだと考えました。

地域・エリアであれば、地域ごとの自転車利用に意味のある違いに気づくことができればエリアごとの施策を考える材料にできるかもしれません。

利用時の走行距離と自転車ステーションの設置場所がわかると、非会員・会員ユーザーのターゲット像の分類を考える材料となり、量的なユーザー理解に繋げることができる可能性があります。

上記のように仮説ベースで、精度改善にあったら良さそうなデータを考えることが大事ですし、何より分析の醍醐味であるように思いました。

まとめ

  • 分析の初期段階では、目的変数や説明変数を設定するために要約統計量や可視化（ヒストグラム、相関行列、バイオリンプロットなど）を行い、データの特徴を把握する。
    • Node-AI では、要約統計量はデータカードから確認可能であり、相関行列やバイオリンプロットなどの可視化カードもある。
  • モデル評価時には、何度か説明変数の組み合わせを入れ替えるが、精度が比較的良かった理由/悪かった理由を探るために可視化などのアプローチから確認する。
  • 時系列データならではの精度改善のコツとして、休日情報やトレンド情報を組み込むことがあげられる。
    • Node-AI では、休日情報抽出カードがあり、スムーズにデータ追加することが可能です。