データ分析において、可視化は非常に重要な役割を果たします。データを可視化することで、複雑なデータの傾向や関係性を直感的に理解することができます。この記事では、代表的な可視化手法である 散布図、ヒストグラム、相関分析、相関行列 の解釈方法について解説します。

この記事を読む前に

データ分析における基礎をより理解したい方は、以下の記事を先に読むことをおすすめします。

データ分析におけるゴール・課題の設定

データ分析プロセスの全体像

時系列データの基本概念

可視化の役割

データ分析の初心者の多くは、複雑な数式やアルゴリズムに圧倒されがちです。また、Node-AI を利用する際には、モデルや前処理のパラメータの試行錯誤を闇雲にやってしまいがちです。

しかし、可視化はデータの全体像を直感的に理解し、分析を進めるための道標となります。

また、可視化する際の具体的なメリットは例えば下記が考えられます。

• 前処理の設計やパラメータのチューニングを効率的に行うことができる

• 分析チームやステークホルダーとの共通認識を形成し、コラボレーションを促進する

• データの異常を発見し、早期に対処することができる

例えば、売上データの表を見るだけでは、商品の売れ行きが良いのか悪いのか、どんな傾向があるのか、なかなか分かりません。しかし、ヒストグラムで売上データを可視化すると、売上の分布が一目で分かります。また、商品の価格と売上の関係を調べたい場合、散布図を使うことで、価格が高いほど売上が多いのか、それとも逆に安価な商品の方が売れるのか、一目瞭然です。

現実はこのように簡単に解釈が得られるものばかりではないと思いますが、可視化という分析手段を用いることで複雑なデータを分かりやすく表現したり、分析のアイデアを生み出すことが可能となります。

可視化の思考プロセス

データの可視化は、単にグラフを描くのではなく、データに対する仮説を検証するプロセスです。可視化によって得られた知見から、新たな仮説を立て、さらに分析を進めることができます。ここでは可視化の思考プロセスの 1 つを示します。例えば、あるオンラインショップの売上データを使って、商品の価格と売上の関係を分析したいとします。

ステップ1. 仮説を立てる

データからどのような知見を得たいのか、仮説を立てます。

例えば、「商品の価格が高いほど売り上げは多くのなるのか？」のように、具体的な疑問を仮説の形で表現します。

ステップ2. 変数の意味を理解する

可視化する変数の意味を理解し、一般的に考えられる傾向を洗い出します。

例えば、「商品の価格」と「売上」の関係を調べる場合、以下のようなことが思い浮かびます。

• 商品の価格が高いほど、売上も高くなる傾向があるのか？

• 商品の価格が高いほど、顧客は購入をためらう可能性があるのか？

• 商品の価格が安いほど、売れ行きがいいのか？

ステップ3. 重要な仮説を選択する

立てた仮説の中から、検証すべき重要なものを選びます。すべての仮説を検証するのは現実的ではありません。データ分析の目的に沿って、重要な仮説を絞り込みます。

戦略として、「ほぼ自明な仮説ではあるが、本当にデータがそうなっているのかを検証する」「シンプルでわかりやすい仮説から検証する」といったものがあげられます。これは、より複雑な仮説を検証する際にベースとなるのはこのような基礎的な仮説が正しいことが前提になるケースが多いためです。

ステップ4. 適切な可視化手法を選択する

選んだ仮説を検証するために、適した可視化手法を選択します。また、可視化手法ごとに適している情報が異なるため、目的に合った可視化の種類を選びましょう。

例えば、本記事の後半で紹介する 4 つの手法の特徴は下記です。

• 散布図
  ケース: 2 つの変数の関係性を視覚的に理解したい場合
  特徴: 2 つの変数の関係性を点で表現し、その分布を表示することで、2 つの変数の相関関係の強さ・外れ値や偏りなどを直感的に理解することができます。

• ヒストグラム
  ケース: 1 つの変数の分布を理解したい場合
  特徴: データの値を階級別に集計し、その度数を棒グラフで表示することで、1 つの変数のデータの分布・外れ値や偏り・期間別の分布の変化などを直感的に理解することができます。

• 相関分析
  ケース: 複数の変数間の相関関係を数値的に評価したい場合
  特徴: 2つの変数の関係性を数値で表すことで、相関関係の強さと方向を定量的に評価することができます。目的変数に対する相関が強ければ、説明変数として選択する 1 つの根拠にすることができます。

• 相関行列
  ケース: 複数の変数間の相関関係を視覚的に理解したい場合
  特徴: 複数の変数の相関関係を、色の濃淡で表現した行列で表します。相関関係が強いほど色が濃くなり、相関関係が弱いほど色が薄くなります。説明変数同士が強く結びついてる変数を選択するとモデルの精度低下につながる可能性があるため、そのような変数選択に役立てることができます。

ステップ5. 可視化を実行する

選択した可視化手法を適用し、グラフを作成します。

例えば、プログラミング言語である Python を用いてグラフを作成することが可能です。プログラミング以外では、エクセルや BI ツール、ノーコードで利用可能な Node-AI などの分析ツールが選択としてあがります。

グラフを作成する際には「縦軸」と「横軸」に何を指定すると良いかを考えるとよいでしょう。
例えば、商品の価格と売上を分析する場合、グラフで表現したいことが変わります。

• 縦軸に売上、横軸に価格 を設定すると、価格と売上間の関係が直感的に理解できます

• 縦軸に売上、横軸に販売日 を設定すると、商品の売上の時間的な変化を把握できます

ステップ6. 解釈と考察をする

作成したグラフを解釈し、仮説が正しいかどうかを考察します。グラフから読み取れる傾向やパターンを分析し、仮説を検証します。仮説と検証に関しては、「Node-AI で実践」 項目で Node-AI の可視化カードを用いて解説します。

しかし、一度の可視化で上手くいくことは少ないでしょう。異なる可視化手法を試すためにステップ 4 に戻ることが必要があるかもしれませんし、場合によっては可視化のための前処理を実施したのちにステップ 5 に戻る必要があるかもしれません。

ステップ7. 次のステップへ

仮説が正しい場合は、前処理や変数選択などを検討し、さらに分析を進めます。

仮説が正しくなければ、別の仮説を検証するためにステップ 3 に戻ったり、新たな仮説を立てて検証を繰り返すためにステップ 1 から再スタートします。

これら可視化ための繰り返しの作業は非常に大変ですが、データ分析においてデータの理解を深めるための重要な試行錯誤になりますのでめげずに頑張りましょう！

Node-AI で実践

では、理論を学んだところで Node-AI で実践してみましょう。

可視化手法ごとの実践に入る前に、取り扱うデータについて説明します。Node-AI では、分析対象のデータを「データカード」と呼んでいます。ここでは公開データの 「シェアサイクル利用の総台数予測（クイックスタート用）」 を使用します。

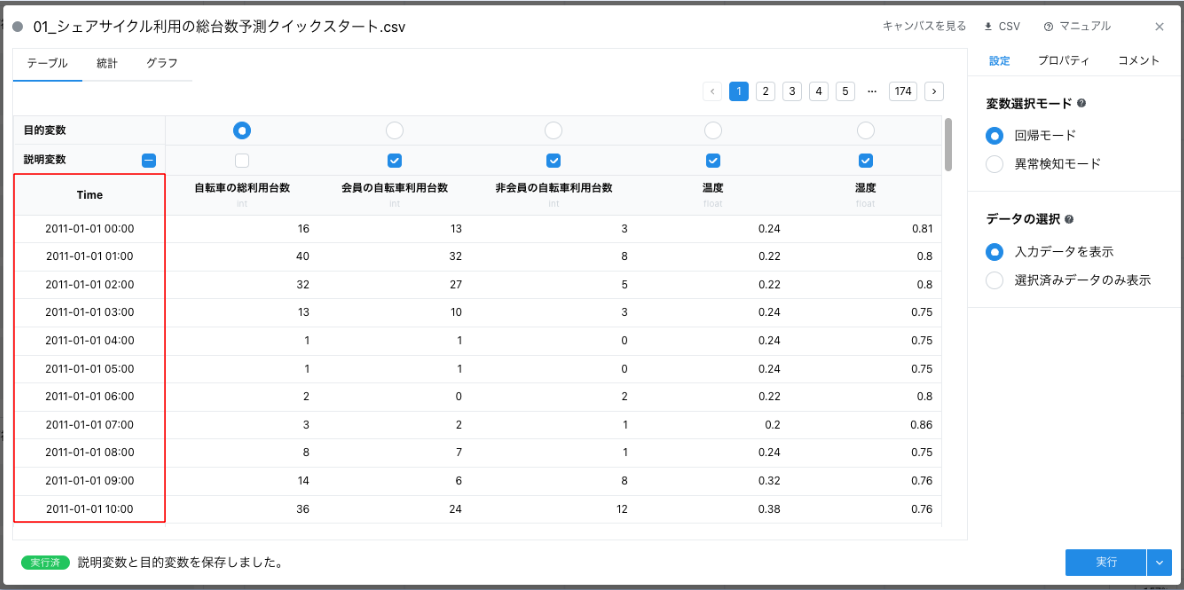
データカードを開くと、データに含まれる変数が表形式で表示されます。 このデータには以下の変数があります（画像の赤枠部分）。

• 「自転車の総利用台数」
• 「会員の自転車利用台数」
• 「非会員の自転車利用台数」
• 「温度」
• 「湿度」

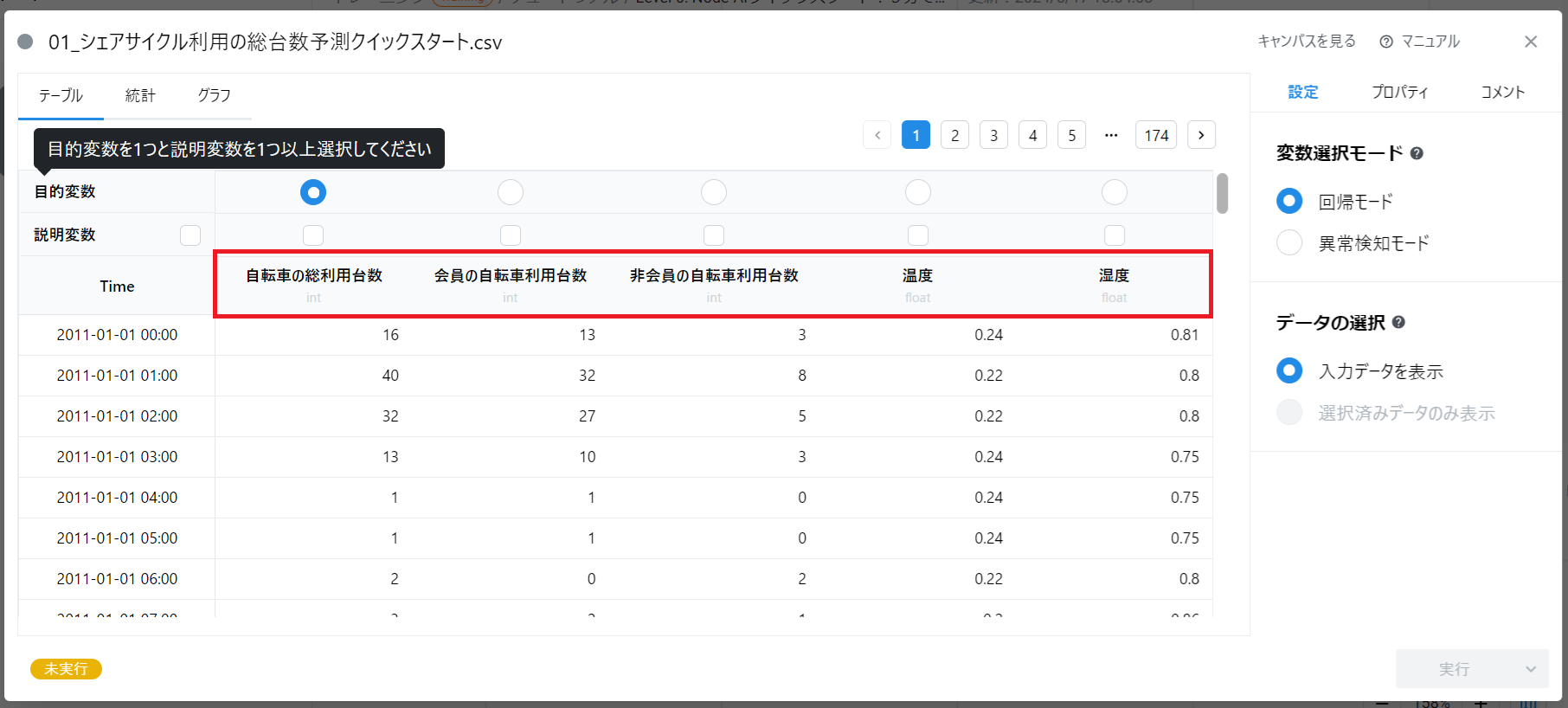
このデータはワシントン D.C.で取得されたシェアサイクルのデータです。 国や文化によってシェアサイクル事情は異なるでしょうから、そういった理解を深めることも必要となります。

ここでは目的変数を「自転車の総利用台数」として、目的変数を精度高く予測する営みを想定しています。その中で精度をより向上させるための有用な説明変数を見つけるために、仮定を立ててそれぞれの可視化による検証をしていきたいと思います。

散布図

概要

ユースケースとして、2 つの変数の関係性を視覚的に理解したい場合に利用されます。

特徴として、2 つの変数の関係性を点で表現し、その分布を表示することで、2 つの変数の変数相関関係の強さ・外れ値や偏りなどを直感的に理解することができます。

※ マニュアル：散布図

仮説と検証

ここでは、「自転車の総利用台数」と「湿度」の関係に着目します。仮説として、「湿度が高い日は、自転車の総利用台数が減るのではないか？」 ということが考えられます。なぜならば、「湿度が高い日もしくは時間帯は、雨が降りやすくなる結果、自転車に乗ることをためらう人が増える可能性がある」 からです。

散布図カードをキャンバスに配置して、シェアサイクルのデータカードから接続します。散布図では、「横軸とするカラム」と「縦軸とするカラム」を選択します。

仮説をもとに、湿度が変化するとどのように自転車の利用台数が変化することをみたいので、横軸に「湿度」、縦軸に「自転車の総利用台数」を選択して実行します。

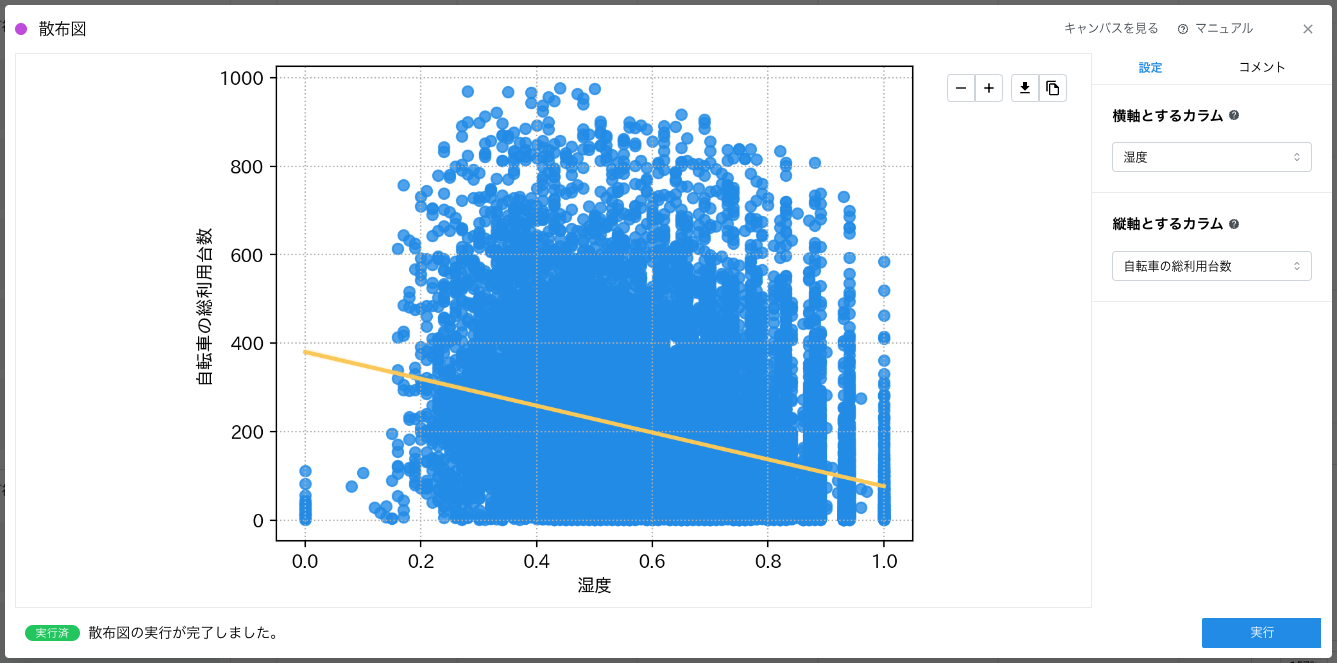
この可視化結果から、湿度 0.2 から 1.0 に向かって徐々に青い範囲（総利用台数がポイントされています）が小さくなっていることがわかります。また、黄色線は回帰線となっていて、「湿度」があがるにつれて「自転車の総利用台数」が減少していく特徴が現れています。これらのことから、仮説は正しそうであること、結果として 「自転車の総利用台数」と「湿度」には相関があるため説明変数として有用であることが言えます。

ヒストグラム

概要

ユースケースとして、1 つの変数の分布を理解したい場合に利用されます。

特徴として、データの値を階級別に集計し、その度数を棒グラフで表示することで、1 つの変数のデータの分布・外れ値や偏り・期間別の分布の変化などを直感的に理解することができます。

※ マニュアル：ヒストグラム

仮説と検証①

ここでは、「自転車の総利用台数」に着目します。仮説として、「シェアサイクルの利用台数は年ごとに増加する傾向にあるのではないか？」 ということが考えられます。なぜならば、「年々、健康志向やサービスの認知度が高まった結果、シェアサイクルサービスを利用する人が増える可能性がある」 からです。

ヒストグラムカードをキャンバスに配置して、シェアサイクルのデータカードから接続します。ヒストグラムでは、「対象カラム」の選択と「ヒストグラムのビン数」を入力します。「ヒストグラムのビン数」とは、ヒストグラムで可視化する際に値をどの程度の粒度でまとめて、グラフを作成するかを指定する数値です。

仮説をもとに、対象カラムを「自転車の総利用台数」、ヒストグラムのビン数を「30」に設定して実行します。

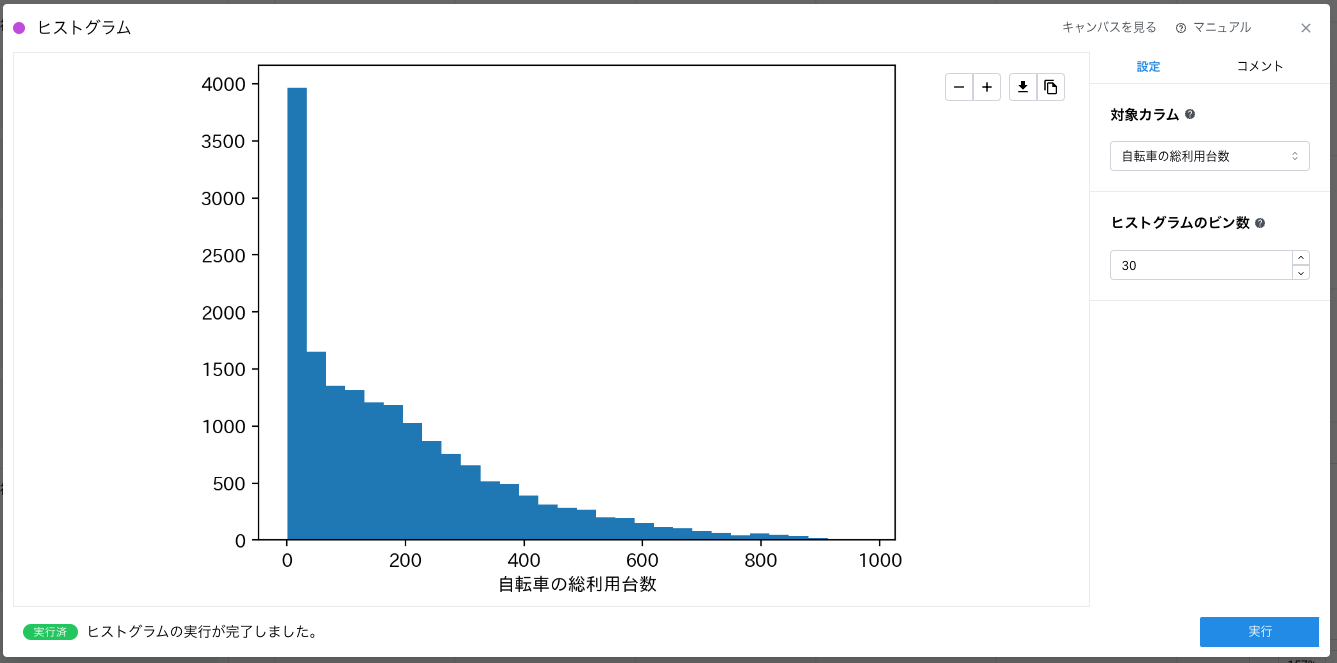
この可視化結果から、自転車の総利用台数は 0 ~ 20 台のレコードが 4000 ほどあり、800 台に向かって徐々にレコード数が減っていることです。これは仮説が間違っていたのでしょうか？仮説が間違っていると判断する前に、仮説に沿った可視化ができているか一度確認してみましょう。

今回扱っているシェアサイクルのデータをよく見ると 1 時間ごとのレコードになっています。このため、上記の可視化結果は 1 時間ごとに総利用台数がどの程度分布しているかを見ていたことになります。

検証したかった仮説は 「シェアサイクルの利用台数は年ごとに増加する傾向にあるのではないか？」 でした。そこで検証するためにデータの前処理として、「カスタム前処理」と「データ分割」を行なってみます。

仮説と検証②

カスタム前処理では「データを日ごとにまとめて、それぞれの日の合計を計算して、1時間ごとのデータを1日ごとのデータに変換する」、データ分割では「5:5 の比率でデータを分割する」を実行します。

カスタム前処理カードとは、Python というプログラミング言語で Node-AI で実装されていない処理を実現できる自由度の高いカードです。Node-AI 上で「データを日ごとにまとめて、それぞれの日の合計を計算して、1時間ごとのデータを1日ごとのデータに変換する」という処理を実現するカードはないため、カスタム前処理カードを使用しています。

※ マニュアル：カスタム前処理

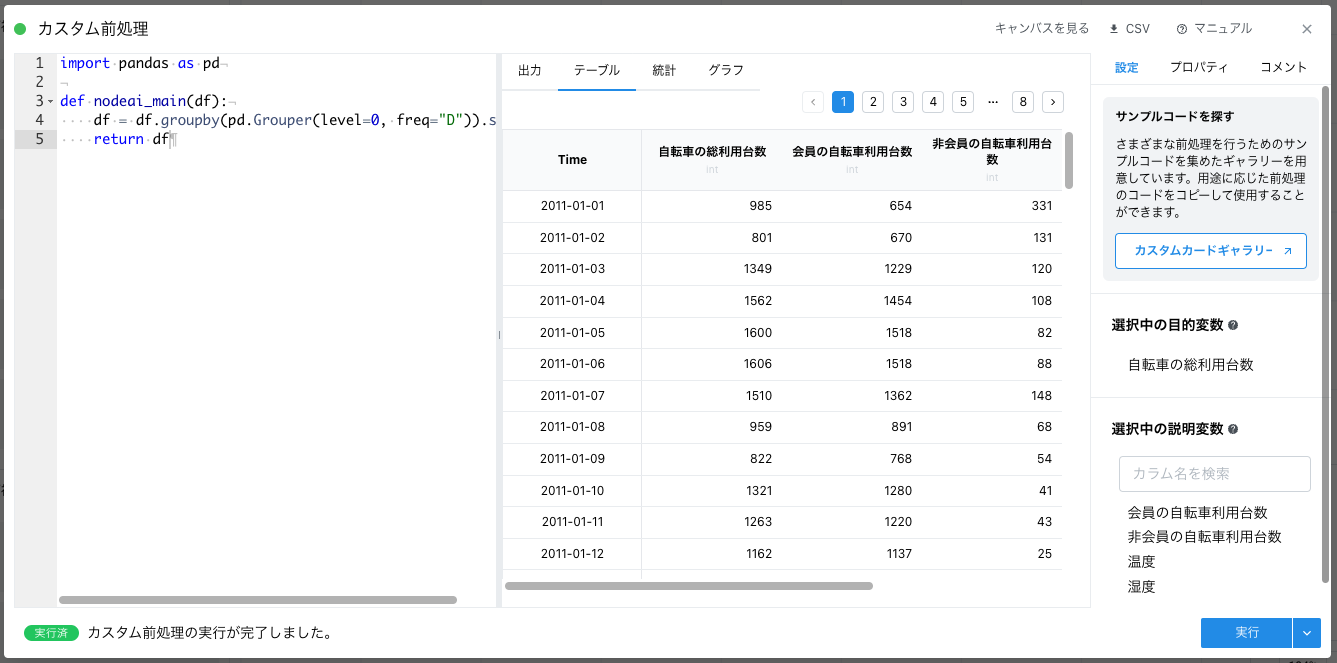
今回実施したカスタム前処理を試した場合は、こちらになります。

import pandas as pd

def nodeai_main(df):
    df = df.groupby(pd.Grouper(level=0, freq="D")).sum()
    return df

また、本来モデルの構築ために学習データと評価データに分割する意図で使用する「データ分割カード」ですが、今回は加工したシェアサイクルのデータを特定の比率で分割するために使用しています。

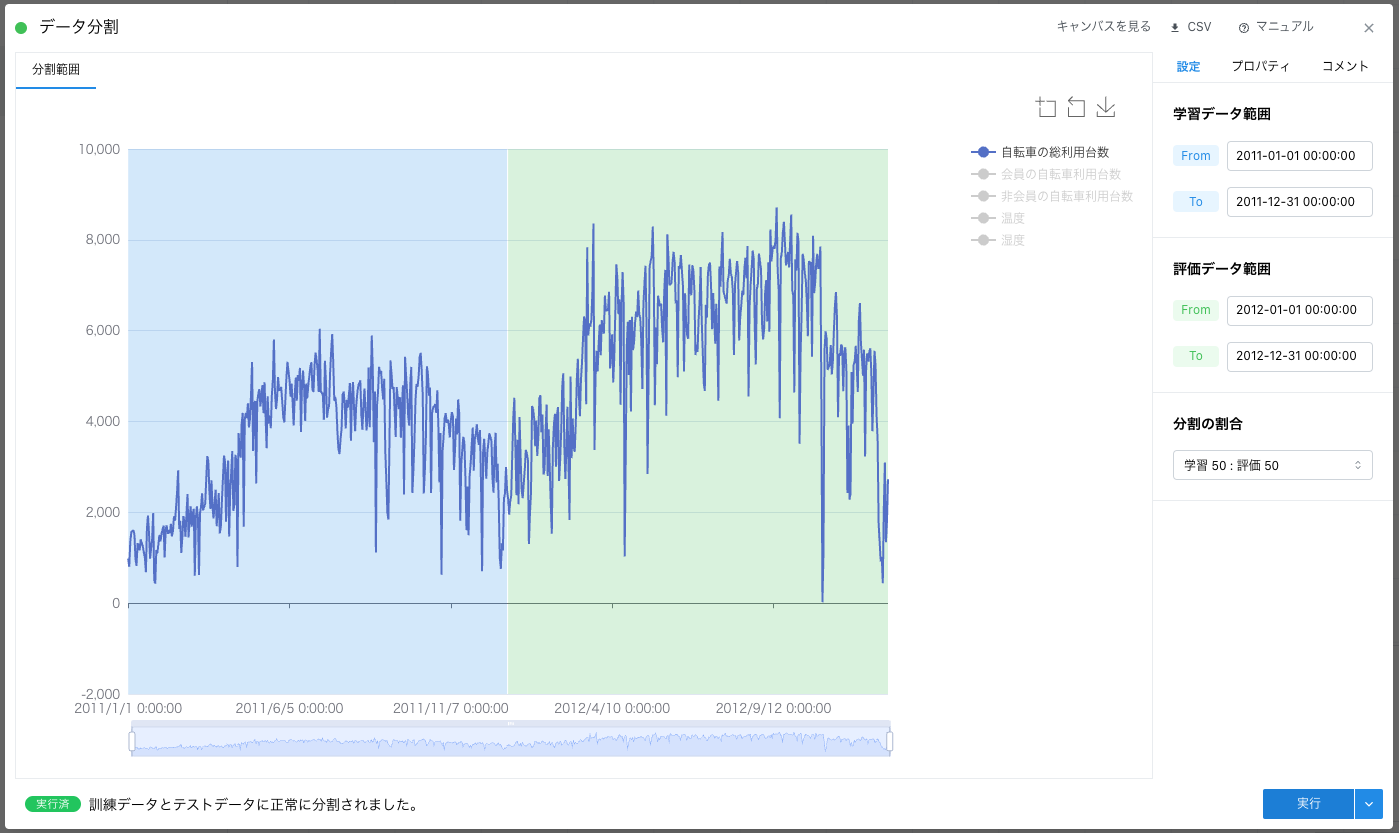
加工したシェアサイクルのデータを 5:5 の比率で分割したものをそれぞれ可視化した結果はこちらです。

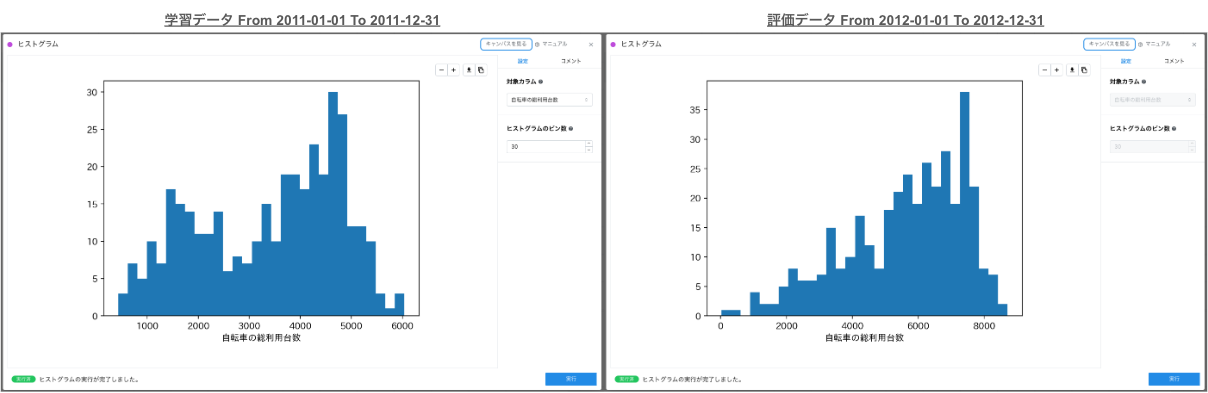
この可視化結果から、学習データである 2011 年のデータでは 「1 日の自転車の総利用台数」 は 4500 台付近が多いのに対して、評価データである 2012 年のデータでは 7500 台付近が多くなっていることがわかります。これらのことから、仮説は正しそうであること、そして 自転車の総利用台数の分布が 4000~5000 台付近から 7500 台付近にシフトしていることが言えます。

このような長期的にみた時の数値の上昇下降を「トレンド」と言います。一般的にこのようなトレンドが見えた場合には下記のような選択肢が存在します。

• トレンドを捉えることができるモデルを使用する

• トレンド成分を取り除く

• トレンド成分を特徴量化する

また、「トレンド」については下記の記事でも一部扱っていますので、ご参考ください。

時系列データの基本概念

相関分析

概要

ユースケースとして、複数の変数間の相関関係を数値的に評価したい場合に利用されます。

特徴として、2 つの変数の関係性を数値で表すことで、相関関係の強さと方向を定量的に評価することができます。目的変数に対する相関が強ければ、説明変数として選択する 1 つの根拠にすることができます。

仮説と検証

ここでは、「自転車の総利用台数」と「気温」「湿度」に着目します。仮説として、「気温が高いほどシェアサイクルの利用台数は増加する傾向にあるのではないか？」 ということが考えられます。なぜならば、データを正規化した下記のグラフから 「気温は四季によって変化しており、気温が高くなるにつれて、シェアサイクルサービスを利用する人が増えている」 からです。

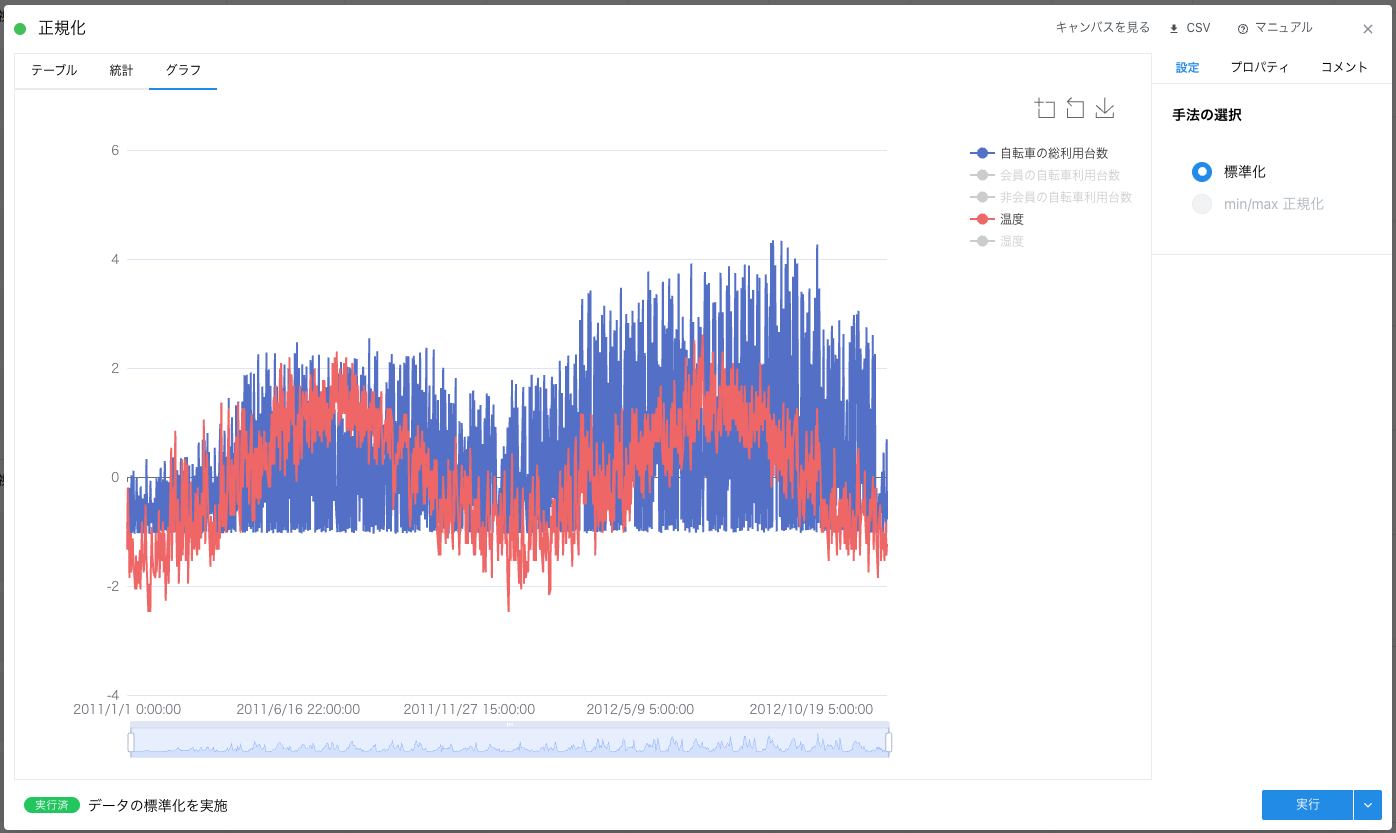
グラフから「自転車の総利用台数」と「気温」の関係を直感的に理解できたので、ここでは定量的に関係性を見てみます。グラフから 「自転車の総利用台数」と「温度」には正の相関がありそうです。また、散布図から 「自転車の総利用台数」と「湿度」に負の相関がありそうだとわかっているため、湿度についても同様に定量的に見てみます。

相関分析カードをキャンバスに配置して、正規化カードから接続します。相関分析カードは、「適用カラム」を選択します。選択するのは目的変数に対して相関を計算したい変数となるため、ここでは「温度」と「湿度」を選択して実行します。

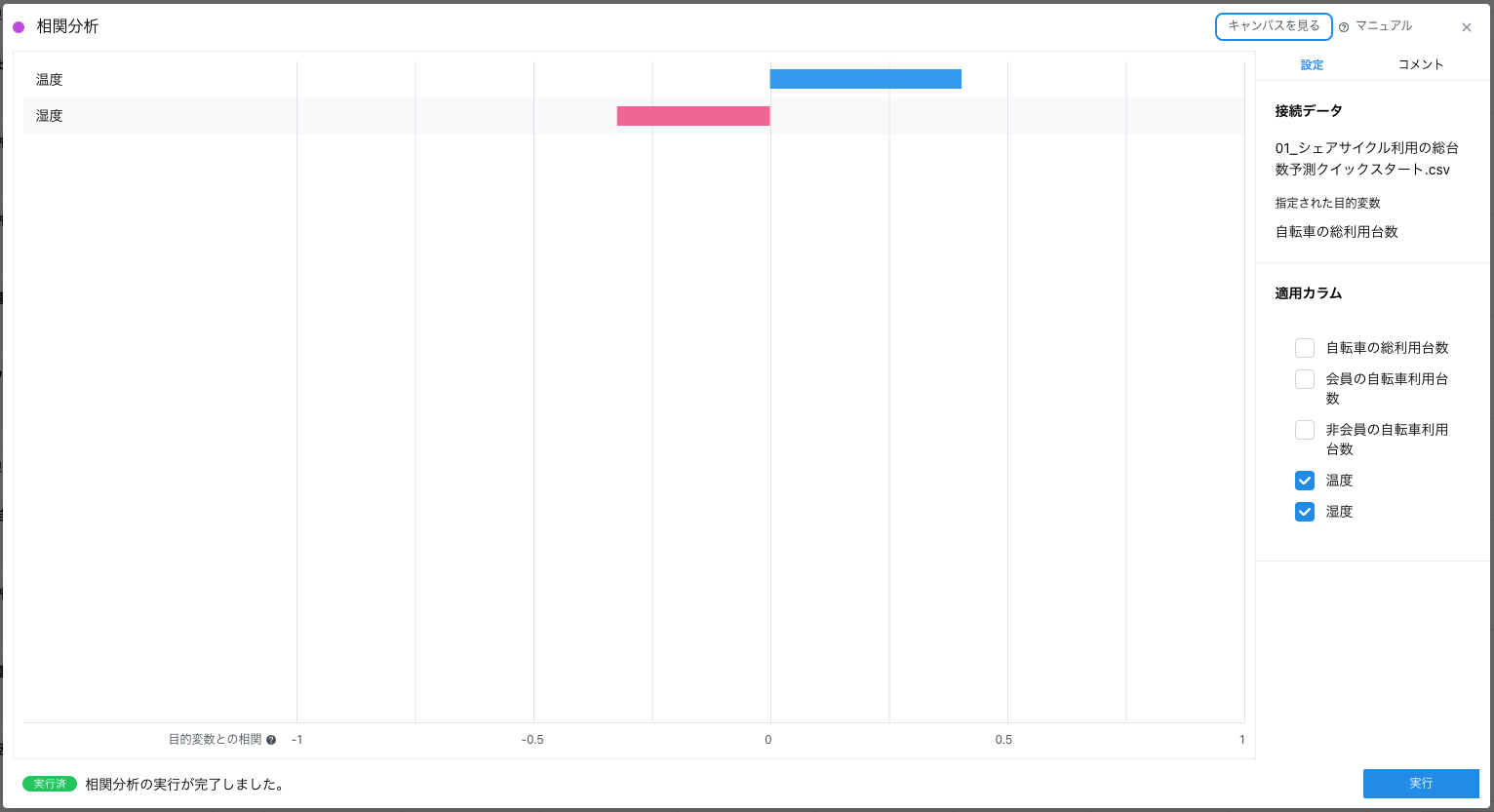
この可視化結果から、「自転車の総利用台数」と「温度」には 0.4 の正の相関があり、「自転車の総利用台数」と「湿度」には 0.3 の負の相関があることがわかります。これらのことから仮説は正しそうであることが言える一方で、年ごとに利用台数が増えている傾向がある（トレンドがある）ことや 1 時間ごとのデータであることから、「自転車の総利用台数」は単純に「気温」や「湿度」だけで説明できるものではなく、他の様々な要因が影響し合っている可能性が高いと言えます。

さらに、これらの変数の相関がそれほど強くないことから、モデルの精度向上に寄与しない可能性も考えられます。特に、相関が低い変数を説明変数として採用することは、モデルが本来のパターンを学習できずに精度低下につながる可能性もあります。そのため、これらの変数を説明変数から外すことも選択肢の 1 つとなります。

（「説明変数から外すこと」は選択肢の 1 つであることに注意してください、必ずしも相関が低い場合に説明変数から外さなければいけないわけではありません。）

相関行列

概要

ユースケースとして、複数の変数間の相関関係を視覚的に理解したい場合に利用されます。

特徴としては、複数の変数の相関関係を、色の濃淡で表現した行列で表します。相関関係が強いほど色が濃くなり、相関関係が弱いほど色が薄くなります。説明変数同士が強く結びついてる変数を選択するとモデルの精度低下につながる可能性があるため、そのような変数選択に役立てることができます。

※ マニュアル：相関行列

仮説と検証

ここでは、「会員の自転車利用台数」と「非会員の自転車利用台数」に着目します。仮説として、「会員と非会員の利用する傾向が異なるのでは？」 ということが考えられます。なぜならば、「会員は通勤や通学などに日常的な移動手段としてシェアサイクルを利用するケースが多い一方で非会員は一時的な利用目的でシェアサイクルを利用することが多い」 からです。

相関行列ヒートマップをキャンバスに配置して、データカードから接続します。相関行列ヒートマップは設定するパラメーターはないため、そのまま実行してください。

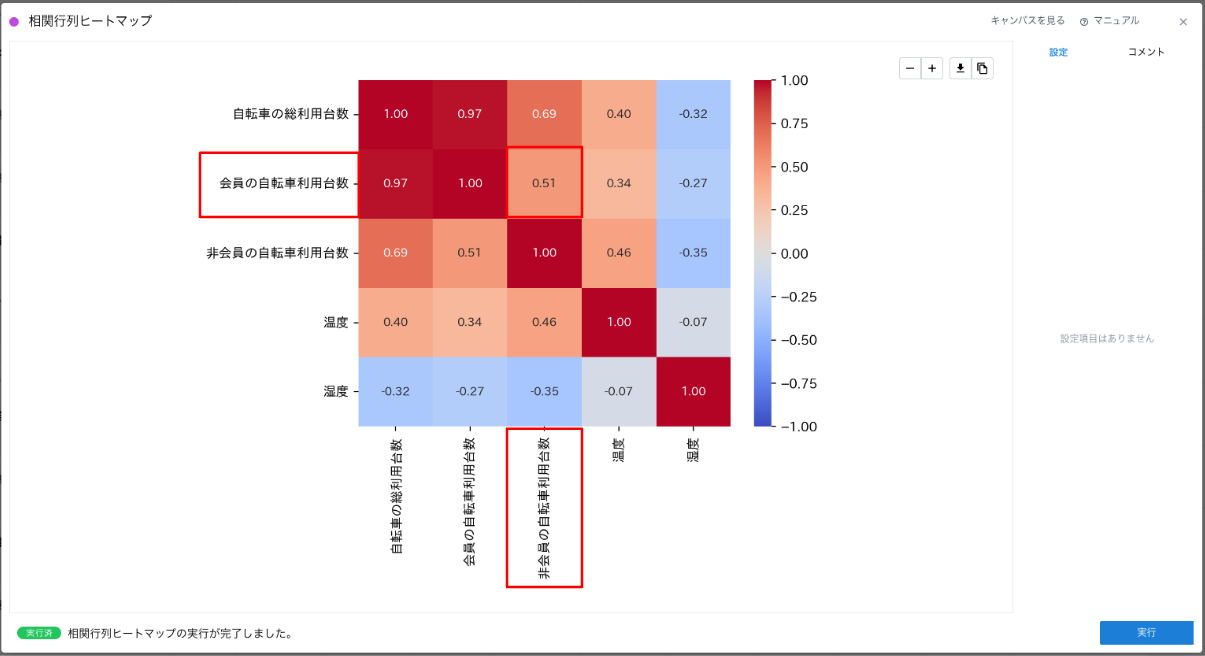
この可視化結果から、「会員の自転車利用台数」と「非会員の自転車利用台数」の相関は 0.51 という正の相関があるが非常に強い相関ではないため、傾向が異なる一面を捉えることができたと言えます。

具体的には、「会員の自転車利用台数」と「非会員の自転車利用台数」が中程度の相関がある場合は、例えば、次のような仮説を考えることができます。

• 会員の利用台数が増えると、非会員の利用台数も増える傾向にある。たとえば、天気が良い日やイベントがある日は、会員も非会員も自転車を多く利用する可能性が高い、と考えます。
• 一方で、必ずしも一致するわけではなく、例えば、特定のプロモーションや割引が会員にのみ適用されると、会員の利用が増えても非会員の利用には影響が少ない場合もあるかもしれません。

さらに「自転車の総利用台数」と「会員の自転車利用台数」、「自転車の総利用台数」と「非会員の自転車利用台数」はそれぞれ 0.97 と 0.69 という強い正の相関があることから 「会員の自転車利用台数」「非会員の自転車利用台数」の 2 つの変数は目的変数である「自転車の総利用台数」に大きな影響を与えていることも言えます。

これらの結果から、「会員の自転車利用台数」「非会員の自転車利用台数」は説明変数として有用であることが言えます。

おわりに

本記事では代表的な可視化手法とその解釈について、理論と実践に分けて説明しました。

ここで説明した可視化手法や解釈はほんの一部でしかありませんが、実際に可視化をしながらデータと向き合う際の手助けになれば幸いです。